AC299R Research Website
Neural Networks for Differential Equations
Contents
import pde_nn.channel_flow as chan
import matplotlib.pyplot as plt
import numpy as np
import utils
# overall hypers
pde_nn = chan.Chanflow()
hypers=pde_nn.hypers
# hypers['nu']=0.001
retau=utils.calc_retau(hypers['delta'], hypers['dp_dx'], hypers['rho'], hypers['nu'])
print('Calculating at Retau={}'.format(retau))
# grid
delta=hypers['delta']
n = 1000
y = np.linspace(hypers['ymin'], hypers['ymax'], n)
delta_y = y[1] - y[0]
u0 = np.ones_like(y)
U_0, U_L = 0, 0
Calculating at Retau=180.0000018
hypers
{'dp_dx': -1.0,
'nu': 0.0055555555,
'rho': 1.0,
'k': 0.41,
'num_units': 40,
'num_layers': 2,
'batch_size': 1000,
'lr': 0.0001,
'num_epochs': 1000,
'ymin': -1,
'ymax': 1,
'weight_decay': 0,
'delta': 1,
'n': 1000,
'in_dim': 1,
'out_dim': 1,
'retau': 180,
'sampling': 'grid',
'activation': 'tanh'}
plt.plot(u0, y)
[<matplotlib.lines.Line2D at 0x11107c0f0>]

# just here for reference.
# reynolds_stress_fn = lambda y, du_dy: -1*((hypers['k']*(np.abs(y)-delta))**2)*np.abs(du_dy)*du_dy
# diffeq = lambda du2_dy2, dre_dy: hypers['nu']*du2_dy2 - dre_dy - (1/hypers['rho']) * hypers['dp_dx']
def handle_boundary(u, i, n):
# careful with boundaries. contains {i-2, i-1, i, i+1, i+2}
# if we step on or beyond the boundary, just set to the boundary (check this assumption!)
# returns u[i-2], u[i-1], u[i], u[i+1], u[i+2] while respecting boundary conditions
if i==0: # far left
return U_0, U_0, u[i], u[i+1], u[i+2]
elif i==1: # second from left
return U_0, u[i-1], u[i], u[i+1], u[i+2]
elif i==n-2: # second from right
return u[i-2], u[i-1], u[i], u[i+1], U_L
elif i==n-1: # far right
return u[i-2], u[i-1], u[i], U_L, U_L
else: # no boundaries
return u[i-2], u[i-1], u[i], u[i+1], u[i+2]
def Gf(u):
n = u.shape[0]
gvec = np.zeros(n)
for i in range(n):
uim2, uim1, ui, uip1, uip2 = handle_boundary(u, i, n)
yim1, yip1 = y[i] - delta_y, y[i] + delta_y
a = (hypers['nu'] / (delta_y ** 2)) * (uip1 - 2*ui + uim1)
fplus = (uip2 - ui) / (2*delta_y)
fminus = (ui - uim2) / (2*delta_y)
b = (1 / (2 * delta_y)) * ((hypers['k'] * np.abs(yip1 - delta)) ** 2) * np.abs(fplus) * fplus
c = (-1 / (2 * delta_y)) * ((hypers['k'] * np.abs(yim1 - delta)) ** 2) * np.abs(fminus) * fminus
d = (-1 / hypers['rho']) * hypers['dp_dx']
gvec[i] = a + b + c + d
return gvec
def dGi_ui(u, i, eps=1e-8):
n = u.shape[0]
uim2, uim1, ui, uip1, uip2 = handle_boundary(u, i, n)
yim1, yip1 = y[i] - delta_y, y[i] + delta_y
a = -2*hypers['nu'] / (delta_y**2)
b = (hypers['k']**2) / (2*delta_y)
fplus = ((uip2 - ui)/(2*delta_y)) + eps
fminus = ((ui - uim2)/(2*delta_y)) + eps
c1 = (np.abs(yip1-delta)**2)
c2 = (fplus**2) * (-1/(2*delta_y)) / np.abs(fplus)
c3 = np.abs(fplus) * (-1/(2*delta_y))
c = c1*(c2+c3)
d1 = -(np.abs(yim1-delta)**2)
d2 = (fminus**2) * (1/(2*delta_y)) / np.abs(fminus)
d3 = np.abs(fminus) * (1/(2*delta_y))
d = d1*(d2+d3)
return a + b * (c + d)
def dGi_uim2(u, i, eps=1e-8):
n = u.shape[0]
uim2, uim1, ui, uip1, uip2 = handle_boundary(u, i, n)
yim1, yip1 = y[i] - delta_y, y[i] + delta_y
a = -((hypers['k'] * np.abs(yim1 - delta))**2) / (2*delta_y)
fminus = ((ui - uim2) / (2*delta_y)) + eps
b = (fminus**2) * (-1/(2*delta_y)) / np.abs(fminus)
c = np.abs(fminus) * (-1/(2*delta_y))
return a * (b + c)
def dGi_uip2(u, i, eps=1e-8):
n = u.shape[0]
uim2, uim1, ui, uip1, uip2 = handle_boundary(u, i, n)
yim1, yip1 = y[i] - delta_y, y[i] + delta_y
a = -((hypers['k'] * np.abs(yip1 - delta))**2) / (2*delta_y)
fplus = ((uip2 - ui) / (2*delta_y)) + eps
b = (fplus**2) * (1/(2*delta_y)) / np.abs(fplus)
c = np.abs(fplus) * (1/(2*delta_y))
return a * (b + c)
def jacobian(u, eps=1e-8):
# returns an entire column of jacobian
# careful with boundaries. contains {i-2, ..}
n = u.shape[0]
jac = np.zeros((n,n))
for i in range(n):
if i == 0:
jac[i,i]=dGi_ui(u, i, eps)
jac[i+1, i]=hypers['nu']/(delta_y**2)
jac[i+2, i]=dGi_uip2(u, i, eps)
elif i==1:
jac[i-1, i] = hypers['nu']/(delta_y**2)
jac[i, i] = dGi_ui(u, i, eps)
jac[i+1, i] = hypers['nu']/(delta_y**2)
jac[i+2, i] = dGi_uip2(u, i, eps)
elif i==n-2:
jac[i-2, i] = dGi_uim2(u, i, eps)
jac[i-1, i] = hypers['nu']/(delta_y**2)
jac[i, i] = dGi_ui(u, i, eps)
jac[i+1, i] = hypers['nu']/(delta_y**2)
elif i==n-1:
jac[i-2, i] = dGi_uim2(u, i, eps)
jac[i-1, i] = hypers['nu']/(delta_y**2)
jac[i, i] = dGi_ui(u, i, eps)
else:
jac[i-2, i] = dGi_uim2(u, i, eps)
jac[i-1, i] = hypers['nu']/(delta_y**2)
jac[i, i] = dGi_ui(u, i, eps)
jac[i+1, i] = hypers['nu']/(delta_y**2)
jac[i+2, i] = dGi_uip2(u, i, eps)
return jac
from tqdm import tqdm
def newton(u0, tol=1e-14, max_iter=int(1e6), eps=1e-8):
u = u0
for it in range(max_iter):
G = Gf(u)
jac = jacobian(u, eps=eps)
delta_u = np.linalg.solve(jac, -G)
u = u + delta_u
max_du = np.max(delta_u)
if it % 100 == 0:
print('iter {}/{}: max delta_u = {}'.format(it, max_iter, max_du))
if max_du < tol:
break
return u
Scipy Root
from scipy.optimize import root
scipy_optimal_res = root(Gf, u0, jac=jacobian, method='lm')
scipy_optimal_res.success
True
u_star = scipy_optimal_res.x
plt.plot(u_star, y)
[<matplotlib.lines.Line2D at 0x101ed4cc88>]
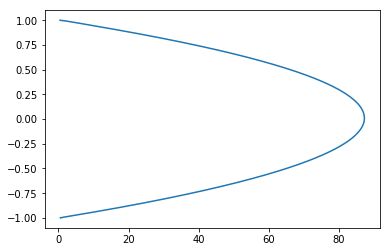
Use Numpy gradient + Scipy Root
ls = np.load('data/mixlen_numerical_u180.npy') #previous result
reynolds_stress_fn = lambda y, du_dy: -1*((hypers['k']*(np.abs(y)-delta)/2)**2)*np.abs(du_dy)*du_dy
diffeq = lambda du2_dy2, dre_dy: hypers['nu']*du2_dy2 - dre_dy - (1/hypers['rho']) * hypers['dp_dx']
def Gf_np(u):
u[0],u[-1]=0,0
du_dy = np.gradient(u, delta_y, edge_order=2)
dre_dy = np.gradient(reynolds_stress_fn(y, du_dy), delta_y, edge_order=2)
du2_dy2 = np.gradient(du_dy, delta_y, edge_order=2)
return diffeq(du2_dy2, dre_dy)
scipy_opt = root(Gf_np, u0, method='lm')
scipy_opt.success
True
plt.plot(scipy_opt.x, y)
plt.plot(ls, y, '--');
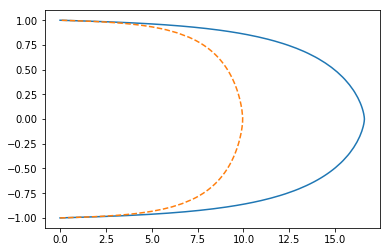
new_kappa = scipy_opt.x
# np.save('data/mixlen_numerical_u180_halfk.npy', new_kappa)
retau 1k
hypers['nu']=0.001
scipy_opt1k = root(Gf_np, scipy_opt.x, method='lm')
scipy_opt1k.success
True
prev1k = np.load('data/mixlen_numerical_u1000.npy')
plt.plot(scipy_opt1k.x, y)
plt.plot(prev1k, y, '--');
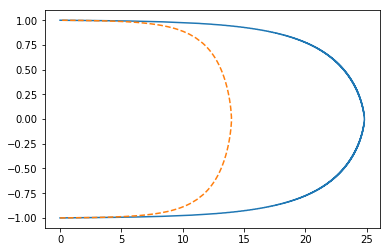
# np.save('data/mixlen_numerical_u1000_halfk.npy', scipy_opt1k.x)
Retau 550
hypers['nu']=0.001818181818
scipy_opt550 = root(Gf_np, scipy_opt.x, method='lm')
scipy_opt550.success
True
prev550 = np.load('data/mixlen_numerical_u550.npy')
plt.plot(scipy_opt550.x, y)
plt.plot(prev550, y, '--');
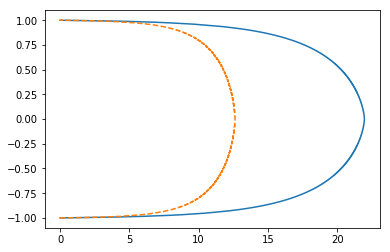
# np.save('data/mixlen_numerical_u550_halfk.npy', scipy_opt550.x)
plt.figure(figsize=(20,10))
plt.plot(ls, y, '-o', label='Retau 180', markersize=0.5)
plt.plot(prev1k, y, '-o', label='Retau 1000', markersize=0.5)
plt.plot(prev550, y, '-o', label='Retau 550', markersize=0.5)
plt.legend()
plt.title('Numerical solution to Channel Flow at Various Re_tau with Mixing Length Model (k=0.41)')
plt.xlabel('< u >')
plt.ylabel('y')
Text(0,0.5,'y')
