Physics-Informed Generative Adversarial Networks for Differential Equations

Background

Consider differential equations of the form

\[F\left(t, \hat{\Psi}(t), \Delta \hat{\Psi}(t), \Delta^2 \hat{\Psi}(t), ...\right) = 0.\]

To set up the problem for Differential Equation GAN (DEQGAN), we let

\[LHS = F\left(t, \hat{\Psi}(t), \Delta \hat{\Psi}(t), \Delta^2 \hat{\Psi}(t), ...\right),\]

and \(RHS = 0.\)

Then we optimize the discriminator ($D$) and generator ($G$) with the gradients:

\[\eta_G = \nabla_{\theta_{g}} \frac{1}{m} \sum_{i=1}^{m} \log{ \left(1 - D \left( LHS^{(i)} \right) \right)},\] \[\eta_{D} = \nabla_{\theta_{d}} \frac{1}{m} \sum_{i=1}^{m} \left[ \log D \left( RHS^{(i)} \right) + \log \left( 1 - D \left( LHS^{(i)} \right) \right) \right],\]

alternating between gradient ascent and descent steps for $D$ and $G$, respectively.

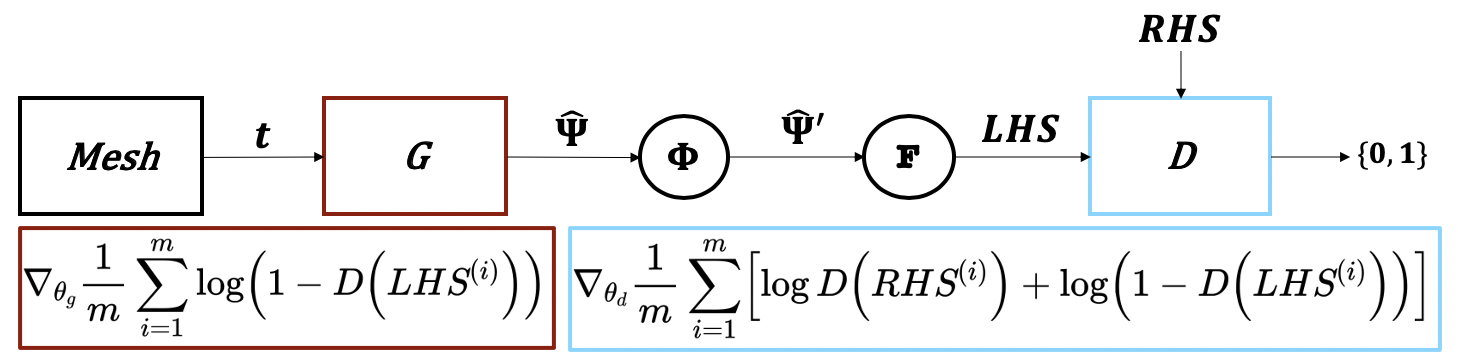Visual representation of DEQGAN formulation.

Results

We obtain orders of magnitude lower error when compared to classic unsupervised neural-network approaches that use traditional loss functions (L1, L2, and Huber).

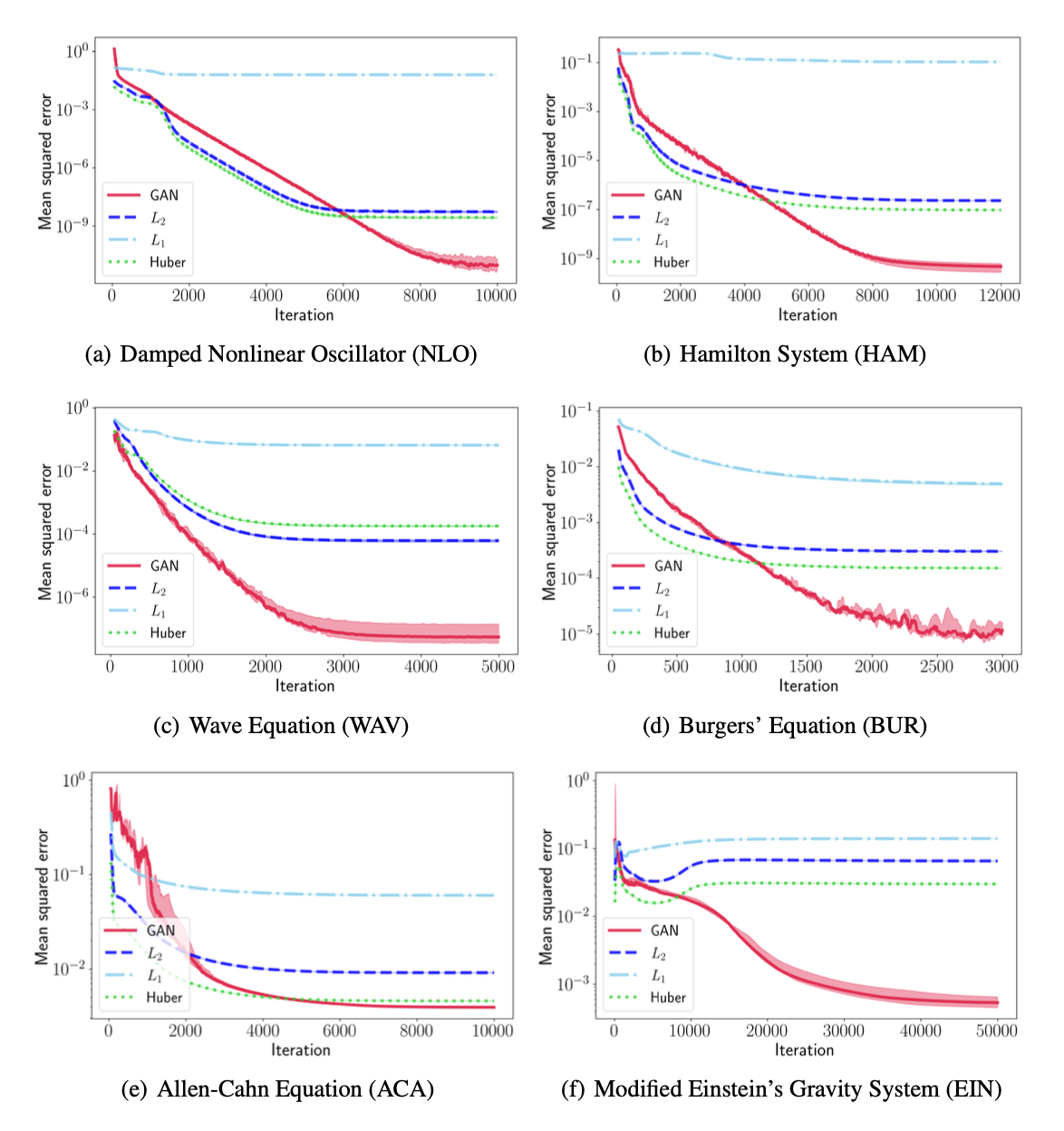Comparison of DEQGAN to traditional physics-informed NNs on various problems.

Further Reading

• My master’s thesis
  • Manuscript
  • Slides
  • Defense
• Preprint paper
• ICML AI4Science paper